고정 헤더 영역
상세 컨텐츠
본문
들어가며..
드래곤 커브가 늘어나는 규칙을 찾은 후, dx,dy를 잘 활용하고 memorization(?)을 잘 하면 쉽게 풀 수 있는 문제였다.
문제 설명은 방향 변화 등이 직관적이지 않았는데, 시작 (2,2)이고 방향 d가 0(왼쪽으로 증가하는 방향)이면서 차원 g=3일 때의 그림 예시를 보고 구현을 할 수 있었다..
(심지어 처음에는 직선이 0차원이 아니라 1차원으로 봐서 차원마다 직선 늘어나는 개수를 잘못 계산했었다ㅠㅠ)
드래곤 커브 초기 정보 저장 및 solution 구성
class Sols{
public:
vector< tuple<int,int,int,int> > curves; // x,y,direction, g (오,위,왼,아래)
int matrix[MAX_MATRIX][MAX_MATRIX];
vector< pair< int, pair<int,int> > > vertexs[MAX_N+1];
int max_row, max_col;
Sols(){
max_row=INT_MIN, max_col=INT_MIN;
for(int i=0; i<MAX_MATRIX; i++){
for(int j=0; j<MAX_MATRIX; j++) matrix[i][j]=0;
}
}curves는 각 드래곤 커브의 초기 시작 정점 (x,y), 방향 d, 차원 g를 tuple의 vector로 저장한다.
matrix는 x,y가 모두 0부터 최대 100까지이므로 생성자에서 최대 크기일 때로 초기화해두고, 드래곤 커브에서 정점을 계산할 때마다 max_row, max_col을 저장해서 정사각형 개수를 셀 때 활용했다.
for(int i=0; i<n; i++){
int x,y,d,g;
cin >> x >> y >> d >> g;
sol->curves.push_back(make_tuple(x,y,d,g));
}
for(int i=0; i<n; i++){
sol->solution(sol->curves[i],i+1);
sol->print();
}
cout << sol->calculate_square() << "\n";입력은 curves에 tuple로 각 드래곤 커브의 정보를 저장한다.
각 드래곤 커브와 드래곤 커브 번호를 solution에 전달해서 각 드래곤 커브에 따른 정보를 solution에서 활용할 수 있도록 했다.
for문에서 각 드래곤 커브를 matrix에 계산한 이후, calculate_square에서 정사각형 개수를 계산했다.
드래곤 커브 규칙 찾기
시작 정점이 (2,2)이고 방향이 0(->), 차원이 3인 경우로 규칙을 찾아보자.
먼저 0차원이다.

0차원은 시작 정점 (2,2)를 기준으로 d만큼 연산했을 때 끝점이 만들어진다.
0차원은 방향 전환이 없이 d를 그대로 사용하고, 끝점 계산된 이후에 방향도 유지되므로 반복문에 포함하지 않고 각 드래곤 커브 처음에 구해줬다.
num이 드래곤 커브 번호일 때, 방향과 정점은 vertexs[num]에 pair<int, pair<int,int> > 순서로 넣어줬다.
int x,y,d,g;
tie(x,y,d,g)=dragon;
// 0차원
matrix[x][y]=num; // dragon curve 번호 넣기
vertexs[num].push_back(make_pair(d, make_pair(x,y)));
matrix[x+dx[d]][y+dy[d]]=num;
vertexs[num].push_back(make_pair(d, make_pair(x+dx[d],y+dy[d])));
max_row=max(max_row, x+dx[d]);
max_col=max(max_col,y+dy[d]);각 정점마다 방향을 넣어야 하는 이유는 3차원까지 만들어보면 알 수 있다..
다음은 1차원이다.
1차원부터는 규칙이 만들어진다. (여기서 방향이 헷갈려질 수 있다)
0차원에서 끝점 정보 d: 0, v: (2,3)을 가져온다.
시계 방향으로 90도 돌렸을 때 만들어진다고 해서 -> 화살표를 시계 방향 90도 돌리면 아래를 가리키니까 d= 0->3인 줄 알았다.

근데 그림을 보면 edge가 위로 만들어진다..?
이해하고 보니, 시계방향 90도라는 의미는 0->1->2->3->0->...으로 바꾸면 된다고 이해하면 됐던 것이다.
따라서 (2,3)에서 d:1을 적용하여 (-1,0)을 더했을 때의 결과 (1,3)이 1차원의 끝점이 된다.
1차원에서의 결과 정점은 1개(count=1)이며, d:1, v: (1,3) 정보를 vertexs[num]에 pair로 넣어준다.
다음은 2차원이다.
1차원에서의 끝점 정보 d:1 v: (1,3)을 가져온다.
1차원에서 방향이 전환되는 방법을 알았으니, d=(d+1)%4로 계산한 방향 2로 (0,-1)을 (1,3)에 더해서 (1,2)를 구한다.
정점 정보 d: 2, v: (1,2)를 vertex[num]에 넣는다.
다음 edge는 무슨 방향 기준으로 계산해서 어떻게 구할 것인가???
일단 2차원에서 정점은 2개 만들어져서 count=2이다.
다음 정점은 vertex 벡터에서 count=1 인덱스의 방향 정보를 가져오면 된다.

d:0이었으므로 시계 방향 90도 계산하면 1이 되어 방금 만든 (1,2)에 (-1,0)을 더하여 (0,2)가 만들어지는 것이다.

이제 2차원에서 만들어진 정점은 2개이고(count=2), d:1, v: (0,2) 정보를 벡터에 넣어준다.
다음은 3차원이다.
3차원부터 각 차원에서 만들어야 하는 정점의 규칙이 만들어진다.
결론부터 말하면 3차원에서 추가되는 정점은 4개이다.
1차원->1개, 2차원->2개, 3차원->4개가 만들어지므로,
count=pow(2, i-1)임을 도출할 수 있다.
따라서 while문을 count가 0이 아닐 때까지 돌리고, 각 정점 만들 때마다 count--를 해주면 다음 단계에서 사용해야 하는 방향 정보를 가져올 수 있다.
// 1차원부터
for(int i=1; i<=g; i++){ //1->1개 추가 2->1개 추가, 3->2개 추가 4->4개 추가
// 1차원 만드는 경우 정점 1개로 만듬
int count=pow(2, i-1); // 만들어야 하는 점의 개수
while(count){
// vertexs의 마지막 정점을 꺼냄
int cd=vertexs[num][count--].first;
int cx=vertexs[num].back().second.first;
int cy=vertexs[num].back().second.second;
// 다음 만들 정점
cd=turn_clock(cd);
int nx=cx+dx[cd];
int ny=cy+dy[cd];
// 마지막 추가한 정점이 끝점
matrix[nx][ny]=num;
vertexs[num].push_back(make_pair(cd, make_pair(nx,ny)));
max_col=max(max_col, ny);
max_row=max(max_row, nx);
}
}이때 nx,ny는 항상 유효한 범위 내에서 만들어짐이 문제에서 설명되었기 때문에, 만들어지는 정점의 유효성을 검사하지는 않았다.
정점을 추가할 때마다 max_row, max_col을 업데이트해줬다.
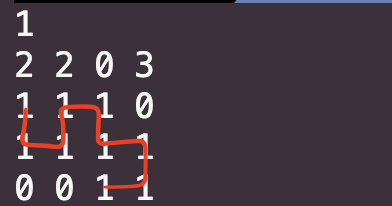
위 그림은 앞선 예시를 앞선 방식대로 구현했을 때 결과이다.
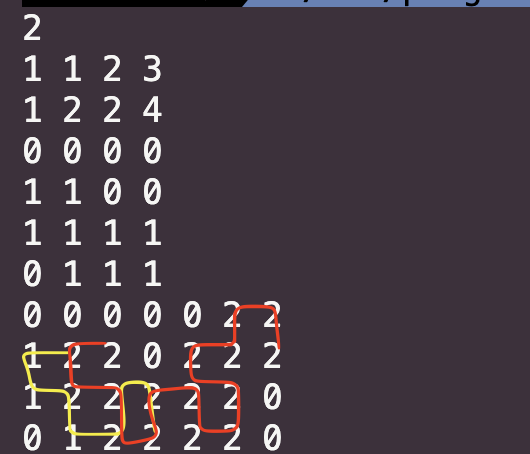
겹쳐서 덮어써지는 부분은 어쩔 수 없지만, 값은 제대로 채워진다.
정사각형 구하기
// 길이 1인 정사각형 (i,j) 기준 (0,0) (0,1) (1,0) (1,1)이 모두 0이 아니어야 함
int rx[]={0,0,1,1};
int ry[]={0,1,0,1};
int calculate_square(){
int sum=0;
// 좌측상단 좌표 가능 범위 0~max_row-1
for(int i=0; i<=max_row-1; i++){
for(int j=0; j<=max_col-1; j++){
bool state=true;
for(int k=0; k<4; k++){
if(matrix[i+rx[k]][j+ry[k]]==0) { state=false; break; }
}
// for문 하고 true 나오면 4개 이루어진것
if(state) sum++;
}
}
return sum;
}정사각형은
11
11
이면 되므로, rx,ry를 위의 코드와 같이 구성했다.
max_row, max_col을 구했으므로 해당 범위에서 크기 1인 정사각형은 좌측상단이 0부터 시작했을 때 (max_col-1,까지, row의 경우 각 정사각형이 1칸을 차지하므로 max_row-1까지를 보면 된다.
각 좌측상단이 (0,0)부터 (max_row-1, max_col-1)까지일 때 rx,ry가 모두 0이 아닌 경우에만 카운팅해주었다.
전체 코드
#include <iostream>
#include <vector>
#include <tuple>
#include <cmath>
#define MAX_N 20
#define MAX_G 10
#define MAX_MATRIX 100
using namespace std;
int n;
// 길이 1인 정사각형 (i,j) 기준 (0,0) (0,1) (1,0) (1,1)이 모두 0이 아니어야 함
int rx[]={0,0,1,1};
int ry[]={0,1,0,1};
// 생성 방향 0: 왼쪽, 1: 위쪽 2: 오른쪽 3: 아래
int dx[]={0,-1,0,1};
int dy[]={1,0,-1,0};
class Sols{
public:
vector< tuple<int,int,int,int> > curves; // x,y,direction, g (오,위,왼,아래)
int matrix[MAX_MATRIX][MAX_MATRIX];
vector< pair< int, pair<int,int> > > vertexs[MAX_N+1];
int max_row, max_col;
Sols(){
max_row=INT_MIN, max_col=INT_MIN;
for(int i=0; i<MAX_MATRIX; i++){
for(int j=0; j<MAX_MATRIX; j++) matrix[i][j]=0;
}
}
void print(){
for(int i=0; i<=max_row; i++){
for(int j=0; j<=max_col; j++) cout << matrix[i][j] << " ";
cout << endl;
}
}
// 0->1, 1->2, 2->3,3->4,
int turn_clock(int d){
return (d+1)%4;
}
void solution(tuple<int,int,int,int> dragon, int num){
int x,y,d,g;
tie(x,y,d,g)=dragon;
// 0차원
matrix[x][y]=num; // dragon curve 번호 넣기
vertexs[num].push_back(make_pair(d, make_pair(x,y)));
matrix[x+dx[d]][y+dy[d]]=num;
vertexs[num].push_back(make_pair(d, make_pair(x+dx[d],y+dy[d])));
max_row=max(max_row, x+dx[d]);
max_col=max(max_col,y+dy[d]);
// 1차원부터
for(int i=1; i<=g; i++){ //1->1개 추가 2->1개 추가, 3->2개 추가 4->4개 추가
// 1차원 만드는 경우 정점 1개로 만듬
int count=pow(2, i-1); // 만들어야 하는 점의 개수
while(count){
// vertexs의 마지막 정점을 꺼냄
int cd=vertexs[num][count--].first;
int cx=vertexs[num].back().second.first;
int cy=vertexs[num].back().second.second;
// 다음 만들 정점
cd=turn_clock(cd);
int nx=cx+dx[cd];
int ny=cy+dy[cd];
//if(nx<0 || ny<0 || nx>=MAX_MATRIX || ny>=MAX_MATRIX) continue;
// 마지막 추가한 정점이 끝점
matrix[nx][ny]=num;
vertexs[num].push_back(make_pair(cd, make_pair(nx,ny)));
max_col=max(max_col, ny);
max_row=max(max_row, nx);
}
}
}
int calculate_square(){
int sum=0;
// 좌측상단 좌표 가능 범위 0~max_row-1
for(int i=0; i<=max_row-1; i++){
for(int j=0; j<=max_col-1; j++){
bool state=true;
for(int k=0; k<4; k++){
if(matrix[i+rx[k]][j+ry[k]]==0) { state=false; break; }
}
// for문 하고 true 나오면 4개 이루어진것
if(state) sum++;
}
}
return sum;
}
};
int main(){
ios_base::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
Sols* sol = new Sols();
for(int i=0; i<n; i++){
int x,y,d,g;
cin >> x >> y >> d >> g;
sol->curves.push_back(make_tuple(x,y,d,g));
}
for(int i=0; i<n; i++){
sol->solution(sol->curves[i],i+1);
//sol->print();
}
cout << sol->calculate_square() << "\n";
return 0;
}
// 0차 드래곤 커브 길이 1인 선분
// 1차 드래곤 커브 = 0차 드래곤 커브 복제해서 끝점 기준으로 시계방향으로 90도 회전하여 연결한 것 끝점: 시작점으로부터 가장 멀리 떨어진 점
// n차 드래곤 커브 = n-1차 드래콘 커브 끝점에 n-1차 드래곤 커브 복제 후 시계 방향 90도 회전하여 연결한 도형
// direction 0: y 증가하는 방향, 1; x 감소하는 방향, 2: x 증가하는 방향. 3: y 증가하는 방향

'PROGRAMMING > Algorithm' 카테고리의 다른 글
| [백준(BOJ)] 14499번: 주사위 굴리기(C++) (1) | 2025.03.12 |
|---|---|
| [백준(BOJ)] 14940번: 쉬운 최단거리 (C++) (0) | 2025.03.11 |
| [백준(BOJ)] 1283: 단축키 지정 (C++) (0) | 2025.03.10 |
| [백준(BOJ)] 2011번: 암호 코드(C++) (0) | 2025.01.04 |
| [백준(BOJ)] 11725: 트리의 부모 찾기(C++) (0) | 2025.01.03 |




